What would you see from a moon revolving in a different plane of orbit and how plausible is this?

Calculations:

Brief description:

In this simulation I have a system consisting of a moon orbiting a planet orbiting a sun. However, the moon's orbital plane is perpendicular to the planet's orbital plane.

Known values:

Moon's mass: 4.7998 * 10²² kg (same as Europa's mass)
Moon's radius: 1.561 * 10⁶ m (same as Europa's radius)
Tilt of moon's axis (relative to orbit): 30 degrees
Sun's mass: 1.989 * 10³⁰ kg (same as our sun's mass)
Sun's radius: 6.95508 * 10⁸ m (same as our sun's radius)
Planet's orbit is the same as Earth's (mean dist.: 1.496 * 10¹¹ m, eccentricity: 0.0167086, etc.)
Planet's mass: 2.3 * 10²⁸ kg
Planet's density: 1330 kg/m³ (same as Jupiter's)

Why did I choose these values?

I made the moon identical to Europa because that way I know that it can exist. I picked Europa over other moons because Europa is pretty small so it will not have much of an effect on the planet. I chose for the moon's axis to be tilted at 30 degrees because that is close to the tilt of Earth's axis (24.5 degrees).

I made the sun identical to our sun and the planet's orbit identical to Earth's orbit to insure that we can see the sun from the moon and that it is bright enough.

I wanted to have the moon's orbit be as big as possible (so the sun clearly appears to change in size), so I needed the planet to have as much mass as possible. This would allow the moon to orbit farther from the planet without being pulled toward the sun. The widely accepted maximum mass of a gas planet (above this mass it will turn into a brown dwarf) is about 17 times the mass of Jupiter (2.847 * 10²⁸ kg), so to be safe I made my planet's mass 2.3 * 10²⁸ kg. I used Jupiter's density for this planet because both Jupiter and this planet are large gas giants.

Calculating how far from the planet the moon can orbit:

The moon's orbit in a planet - moon system can be practically as big as we want, however in this system there is a sun, and therefore a point at which the sun will pull the moon with a stronger force than the planet. This is the limit of how big the orbit can be, so all I need to calculate is when the force of gravity from the sun is equal to the force of gravity from the planet, and that will be the farthest the moon can orbit.

The formula for the force of gravity is:

$$ F = \dfrac{Gm_1\times m_2}{r^2} $$

m₁ - mass of object 1
m₂ - mass of object 2
r - distance between the objects
G - gravitational constant (6.67408 * 10^-11)

So the equation I have is: $$ F_{sun} = \dfrac{Gm_l\times m_s}{r_l^2} = F_p = \dfrac{Gm_l\times m_p}{r_p^2} $$

Both sides can be divided by G * m_l leaving us with:

$$ \dfrac{m_s}{r_l^2} = \dfrac{m_p}{r_p^2} $$

We know the mass of the planet and the sun. We also know that r_l + r_p = distance from the planet to the sun = 1.496 * 10¹¹ m, thus r_l = 1.496 * 10¹¹ - r_p. If we plug those values in, we get:

$$ \dfrac{1.989\times 10^{30}}{(1.496\times 10^{11} - r_p)^2} = \dfrac{2.3\times 10^{28}}{r_p^2} $$

When we solve this equation, we get r_p ≈ 1.45 * 10¹⁰ meters (exact value: 14525161912.737169241916381353714). This is how far the moon can orbit around the planet.

However that is not all I have to look at. To have a stable orbit, the moon has to be within the planet's hill sphere.

The approximate radius of the hill sphere is determined by the following formula:

$$ r_H \approx a(1-e)(\dfrac{m}{3M})^{\frac{1}{3}} $$

r_H - the hill sphere's radius
a - the semi-major axis of the orbiting body's orbit
e - the eccentricity of the orbiting body's orbit
m - the smaller (orbiting) body's mass
M - the larger body's mass

In this case, the eccentricity is negligible, so we can simply consider (1 - e) to be equal to 1. Considering this, and putting the know values in, we get:

$$ r_H \approx 1.496 \times 10^{11} \times (\dfrac{2.3 \times 10^{28}}{3 \times 1.989 \times 10^{30}})^{\frac{1}{3}} $$

Solving this equation, we get r_H ≈ 2.35 * 10¹⁰ meters (exact value: 23456084972.762376712151111026131).

We can see that the maximum radius of the moon's orbit (1.45 * 10¹⁰) is significantly smaller than the planet's hill sphere (2.35 * 10¹⁰). This means that even if the moon orbits as far as the planet's and sun's gravitational pulls will allow, the moon's orbit will be stable.

Finding the barycenter between the sun and the planet:

The planet in this simulation is very big, and therefore will have a noticeable effect on the sun. Both the planet and the sun will revolve around a common point, called the barycenter.

To find this point we need to use this formula:

$$ r_1 = d\times \dfrac{m_2}{m_1 + m_2} $$

r₁ - distance from the center of object 1 to the barycenter
d - distance between the objects
m₁ - mass of object 1
m₂ - mass of object 2

When we put all the values into the equation, we get:

$$ r_1 = 1.496\times 10^{11}\times\dfrac{2.3\times 10^{28}}{1.989\times 10^{30} + 2.3\times 10^{28}} $$

Solving this equation, we get r₁ ≈ 1.71 * 10⁹ meters (exact value: 1710139165.00994).

Finding the planet's radius:

We know the planet's mass and density, so we can find it's volume, from which we can find it's radius.

$$ M = V\times D $$

$$ V = \dfrac{M}{D} $$

M - mass
V - volume
D - density

When we put our values in, we get:

$$ V = \dfrac{2.3\times 10^{28}}{1330} $$

When we solve this, we get V ≈ 1.7293233 * 10²⁵.

The formula to find the radius from the Volume is:

$$ r = (3\times\frac{V}{4\pi})^{\frac{1}{3}} $$

Plugging our values in, we get:

$$ r = (3\times\frac{1.7293233\times 10^{25}}{4\pi})^{\frac{1}{3}} $$

Solving this equation, we get r ≈ 1.6 * 10⁸ meters (exact value: 1.6042148339 * 10⁸).

Calculating the moon's radiative equilibrium temperature:

For this, I said that the moon has no greenhouse effects and it's Bond albedo (the percent of light hitting it that the planet scatters/reflects) is the same as Earth's (0.29).

The formula for the radiative equilibrium temperature (planet's theoretical temperature if it only receives light from its parent star) is:

$$ T^4 = \frac{L(1 - a)}{16\pi d^2o} $$

T - temperature of the planet (in Kelvin)
L - luminosity of the parent star (in Watts)
d - distance between the sun and the planet (in meters)
a - the planet's albedo (the percent of light reflected by the planet)
o - Stefan-Boltzmann constant (5.670373 * 10^-8 W/m²/K⁴)

Since I have to find the temperature multiple times, I made a program where I put in the values and it solves this equation for me. Here it is:

Star's luminosity: * 10 to the power of
Distance between the planet and star: * 10 to the power of
The planet's albedo (between 0 and 1):

Answer:

Having all of these values, I built the scenario in blender, a 3d modeling program. The following is what I got.

Results

The days on the moon are different depending on where it is in its orbit. The major differences are in the 4 following positions:

Orbital position 1:

Orbital position 2:

Orbital position 3:

Orbital position 4:

Sun - the sun (white sphere)
P1 - the planet (red sphere)
P2 - the moon (gridded sphere)

Orbital position 1:

I put a grid on the moon to make it easier to see how the light travels on its surface.

The moon's radiative equilibrium temperature throughout one full orbit in this position ranges from 269.1902392851965 Kelvin to 244.20747462669004 Kelvin (~25 degree K/C difference)

The first day in this orbital position:

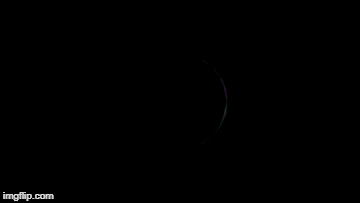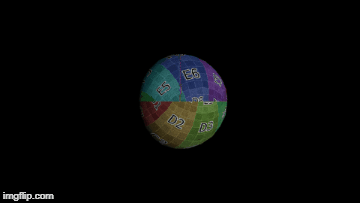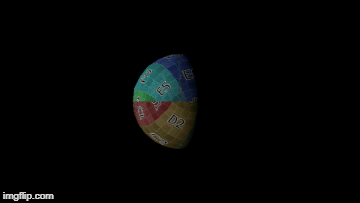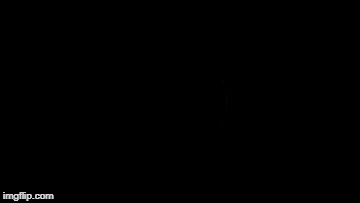
The videos below are synchronized. The one on the left shows where the moon is in its orbit, and the one on the right shows what the moon looks like.

Notice how as time goes on the terminator ("line" that divides the light and shadow) tilts.

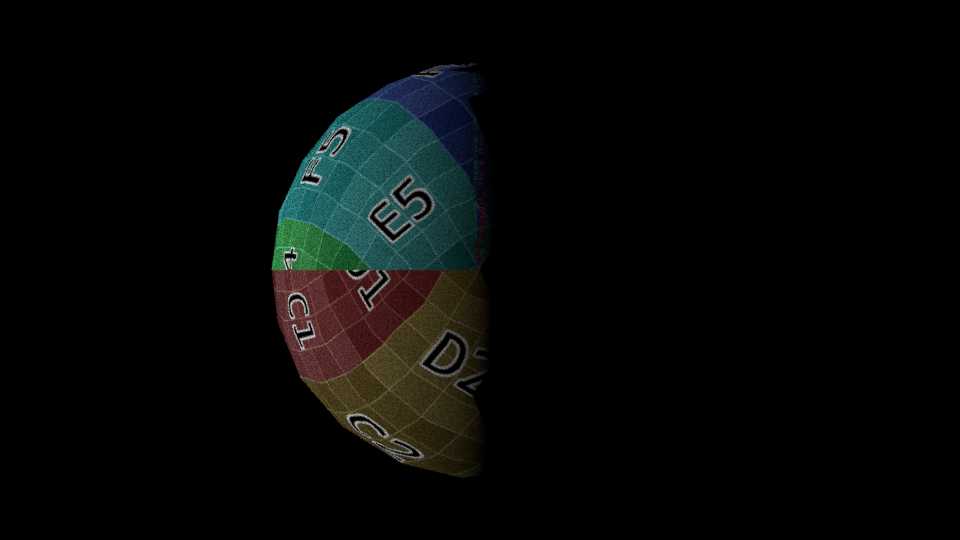
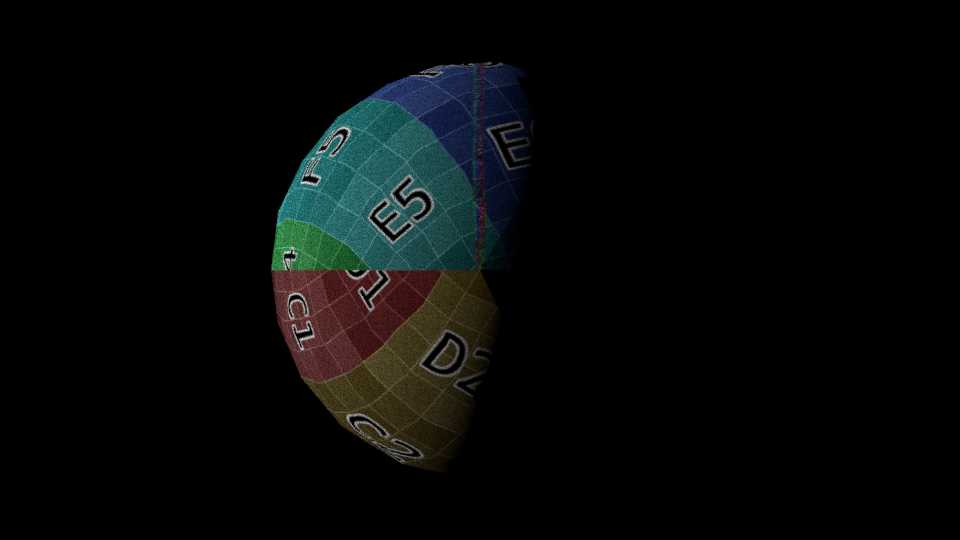
Orbital position 2:

The moon's radiative equilibrium temperature doesn't change a lot in this position, remaining at about 255.78833770226458 Kelvin (~ -17.3 degrees Celsius)

First day in this position:

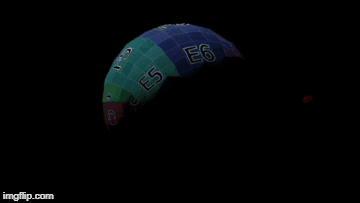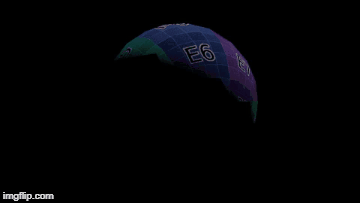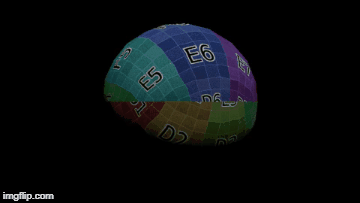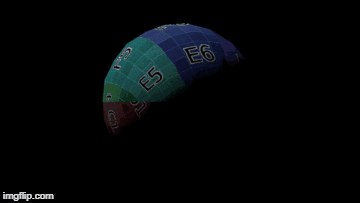
The videos below are synchronized. The one on the left shows where the moon is in its orbit, and the one on the right shows what the moon looks like.

Orbital position 3:

The moon's radiative equilibrium temperature throughout one full orbit in this position ranges from 269.1902392851965 Kelvin to 244.20747462669004 Kelvin (~25 degree K/C difference)

First day in this position:

The videos below are synchronized. The one on the left shows where the moon is in its orbit, and the one on the right shows what the moon looks like.

Orbital position 4:

The moon's radiative equilibrium temperature doesn't change a lot in this position, remaining at about 255.78833770226458 Kelvin (~ -17.3 degrees Celsius)

First day in this position:

The videos below are synchronized. The one on the left shows where the moon is in its orbit, and the one on the right shows what the moon looks like.

Apparent motions of other celestial bodies as observed from the moon.

These two videos are unwrapped 360 degree views of what the sky would look like from a moon orbiting in the same plane and a moon orbiting in a perpendicular plane to that of it's planet.

Symbols:

Red dot - P1
White dot (moving) - Sun
Rectangle - the field of view (how much is seen) of the above videos.
Red lines - P1 travels up/down to these lines (but no lower/higher)

Observations:

P1's vertical motion, in both cases, follows a regular sinusoidal pattern ("wave").
P1 goes up to 60 degrees North and down to 60 degrees South on the normal orbit.
P1 goes up to 30 degrees North and down to 30 degrees South on the tilted orbit.
P1 appears to go faster than the sun on the normal orbit.
P1 appears to go slower than the sun on the tilted orbit.

Why this happens:

As mentioned, in the case with the perpendicular plane of orbit, the moon is tilted 30 degrees relative to it's orbit. This makes the moon's tilt towards P1 be 30 degrees, thus P1 appears to go up/down to the 30 degree latitudes. However when the orbit is tilted to be in the same plane, the moon's axis can not change tilt relative to the sun. Because of this, the moon's axis is now tilted 30 degrees away from P1, or 60 degrees towards P1. This means that P1 will now go up/down to the 60 degree latitude.

Apparent motion of the sun:

The y-axis represents pixels from the center (0 degrees) the sun appears.
The x-axis represents how many full orbits around P1 the moon did (1 - 1 full orbit)
Left image (orange) shows the sun's apparent motion when the moon is on a normal orbit
Right image (green) shows the sun's apparent motion when the moon is on an extremely tilted orbit

In both cases, the pattern can be modeled by a sine function going along a yet greater sinusoidal curve.

If we take into account the sun's apparent shifting up because of P1's and the moon's progression along the orbit around the sun (the sun shifts about 25px up per 1 moon's full orbit around P1), the pattern formed by the motions of the sun is exactly the same that formed by P1, but on a smaller scale.

Analysis:

The difference in the tilt of the terminator turned out to be drastic because the moon was tilted 30 degrees relative to the orbit. Since the orbit was tilted 90 degrees relative to the sun, the tilt of the moon relative to the sun turned out to be 120 degrees! Thus the drastic difference in where the moon is illuminated.

Even though the moon's orbit was very big, it didn't have much an effect on how the moon was illuminated. However, there was significant change in radiative equilibrium temperature on the moon because of this.

In positions 1 and 3, the moon's temperature changes by 25 degrees C. The average change between winter and summer on earth is 14.3 degrees C in the Northern hemisphere and 7 degrees in the Southern hemisphere.

The moon would have 6 seasons - 4 induced by the temperature change because of the moon's huge orbit, and 2 induced by the tilt of the moon's axis. The seasons would go in an order similar to this (starting at position 1):

Northern hemisphere: 1 - 2 - 3 - 4 - 1 - 2 - 3 - 4 - 5 - 5 - 1 - 2 - 3 - 4 - 1 - 2 - 3 - 4 - 6 - 6 - Back to the beginning

Southern hemisphere: 1 - 2 - 3 - 4 - 1 - 2 - 3 - 4 - 6 - 6 - 1 - 2 - 3 - 4 - 1 - 2 - 3 - 4 - 5 - 5 - Back to the beginning

Season 1 - Warm
Season 2 - Normal (~ -17.3 degrees C)
Season 3 - Cold (~ -29.15 degrees C)
Season 4 - Normal (~ -17.3 degrees C)
Season 5 - Very hot (~ 50 degrees C)
Season 6 - Very cold

However, it takes thousands of years for the radiative equilibrium temperature to take effect, so in reality there would probably only be 4 seasons: Seasons 2, 5, 4, and 6.

Despite of this, the orbit does introduce some interesting effects, such as different apparent motions of celestial bodies as observed from the moon, and most likely different gravitational effects.

Conclusion:

A drastically different orbital plane has some visible effects on the moon. For one, the apparent motions of other celestial bodies are affected by such an orbit. Most of the differences seen are there because the moon's orbit has effects on things, such as the relative tilt of the axis, that in turn influence the moon. The lighting and seasonal patterns are however only affected by the tilt of the axis - not the moon. This is mostly because of the limit of how far the moon can orbit. If the moon could orbit much farther, things would get more interesting. Perhaps then a different seasonal pattern would start to occur.

The orbit's greatest effects are on the apparent motions of nearby objects as observed from the moon

New Developments:

Here, I made an equation giving P1 apparent position given P2's axial tilt, axial tilt direction, orbital inclination, and position on orbit (true anomaly).